方向梯度直方图
介绍
传统的目标检测流程可分为三个步骤,第一步是使用滑动窗口和图像金字塔从图片中选择一些区域。第二步是将选择出来的区域转化为人工设计的特征,可称为特征提取。第三步是将这些特征输入分类器进行分类。方向梯度直方图(Histogram of Oriented Gradients)以下简称 HOG,就是一种人工设计的特征,用来简化图像表述的特征描述符。
下图中左边的图片是一只猫,我们不仅可以看出猫身体上的特征、颜色、纹理,而且还能看到背景。右边的图片是使用 HOG 来表示的图片,除了可以看到图中能看出猫的外形,其他的细节包括背景几乎都被去除了,故右边的图片是左边图片的一种简化表示形式。HOG 可以用来表示物体的形状、外形特征,将这些特征输入分类器就可以实现目标的分类。

方向梯度直方图流程
预先归一化(Normalization)
在计算梯度前可对图片归一化(Normalization)处理,归一化的目的是使所有的数值落入到统一的范围内,从而使算法能有更好的表现。
计算梯度
前面提到可以不用预先对图片进行归一化,故可以说 HOG 特征是从计算图像在水平方向和垂直方向上的梯度开始的。图像的梯度计算是使用卷积核对图像进行卷积操作,例如我们可以使用矩阵 [[-1, 0, 1]] 和 [[-1], [0], [1]] 分别与图像上的每个像素进行运算来获得水平和垂直方向上的梯度。
$$
G_x = I \times W_x
$$
$$
G_y = I \times W_y
$$
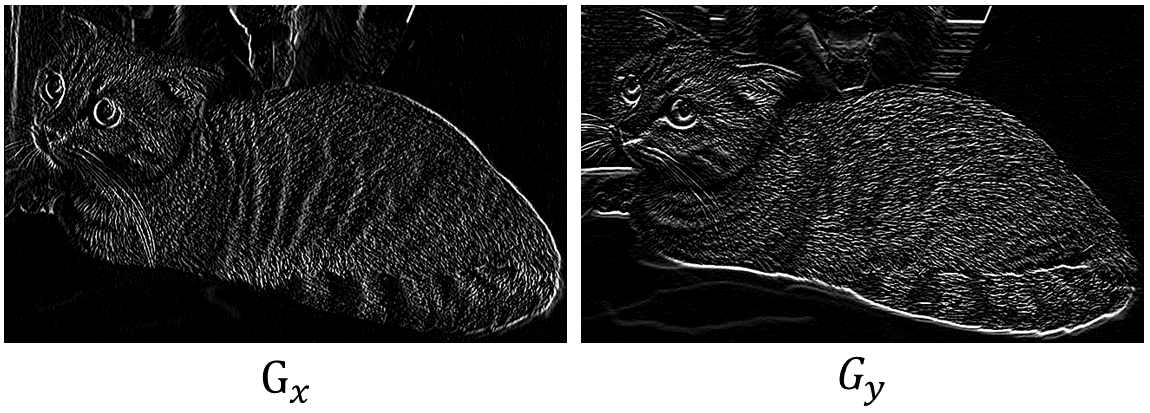
上面两个公式分别计算水平、垂直方向上的梯度 $ G_x $、$\ G_y $。其中 $I$ 是输入图片,$W_x$ 表示水平方向的卷积核,$W_y$ 表示垂直方向的卷积核。下面两张图片给我们展示了经过梯度计算后的图片是什么样子,左图表示计算图片的水平梯度,右图表示计算图片的垂直梯度。相较于原始图片,下面的两张图片中的信息减少了很多,整个 HOG 的过程就是逐步减少图片中的无用信息,只展示给我们感兴趣的特征。
现在已经有了水平方向的梯度 $G_x$ 和垂直方向的梯度 $G_y$,接下来我们要计算梯度的幅值和方向。计算梯度幅值和方向是为了进一步计算方向梯度直方图。
$$ G = \sqrt {G_x^2 + G_y^2} $$
$$ \theta = \arctan \frac{G_y}{G_x} $$
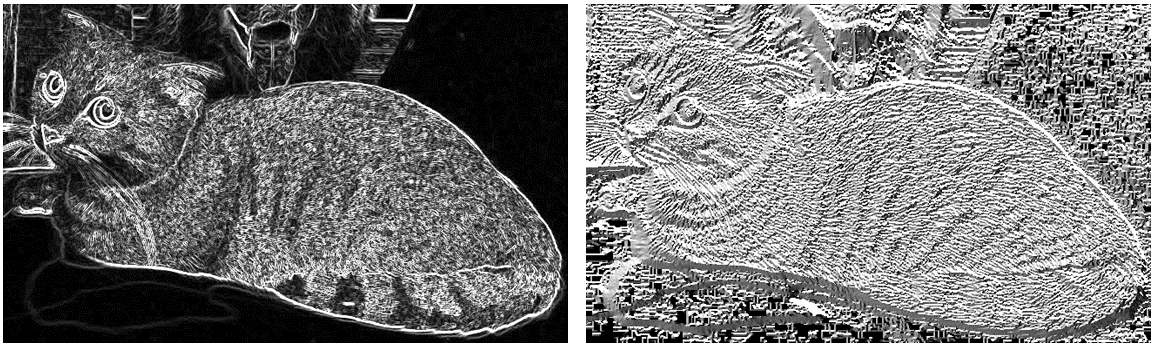
上面的两个公式分别计算每个像素的梯度幅值 $G$ 和梯度方向 $\theta$。下面左图是合并水平、垂直方向上的梯度获得的梯度幅值,可以看到相较于水平、垂直方向上的图片,左图中猫的轮廓更清晰明显。右图表示图片中的梯度方向。
方向梯度直方图
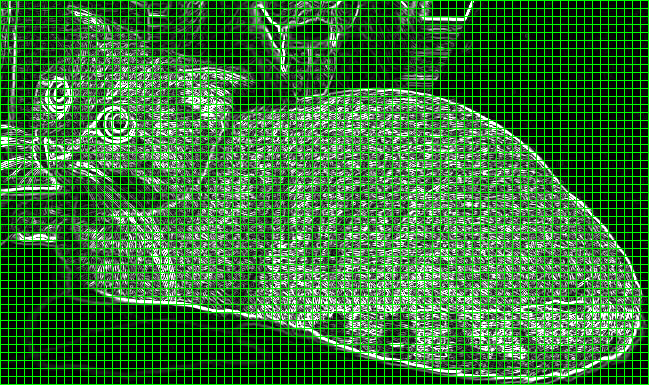
现在我们已经有了梯度幅值 $G$ 和梯度方向 $\theta$,接下来我们就可以计算方向梯度直方图了。在计算方向梯度直方图之前,我们需要将图片分成若干个小方格(Cells),为避免歧义下文皆书写为 Cell 或 Cells 。例如,下图是一张宽高为 $649\times 385$ 的图片,我们将其平均分割成若干个 Cells,每个 Cell 内包含 $8\times 8$ 个像素,所以图片的高被分为 $\lfloor 385\div8 \rfloor = 48$ 份,图片的宽被分为 $\lfloor 649\div8 \rfloor = 81$ 份($\lfloor\quad\rfloor$ 表示向下取整),故整张图片有 $48\times 81$ 个 Cells。
至此我们已经将图片分成许多 Cells,对于每一个 Cell,使用 $G$ 和 $\theta$ 来构建方向梯度直方图。首先我们先选择梯度方向的范围,梯度方向的范围可分为 0 到 180 度(无符号)和 0 到 360 度(有符号),通常使用 0 到 180 度的范围。然后将 0 到 180 度的范围分成 9 个区间(bins),分别为 0 到 20 度,20 到 40 度, 40 到 60 度 …… 160 到 180 度。每个像素都有一个梯度幅值和一个梯度方向,所以方向梯度直方图的计算就是每个像素所对应的梯度方向落在 9 个区间中的哪一个,那么该像素的梯度幅值就在该区间中累加。
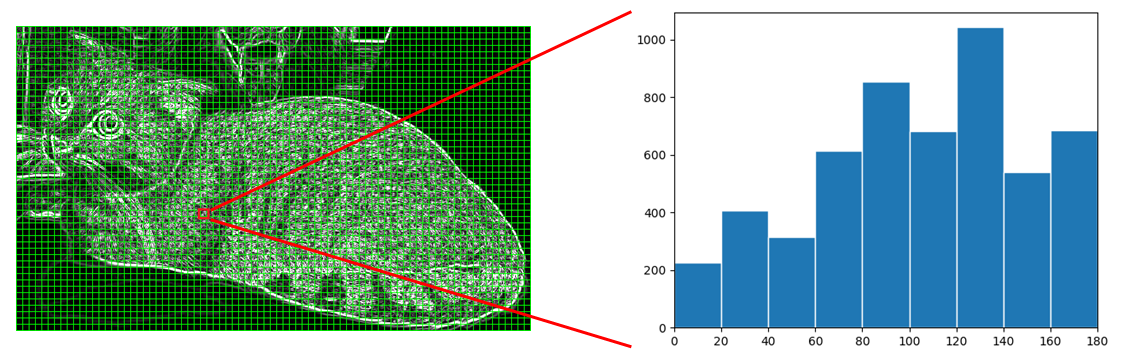
下图是一个计算方向梯度图的例子,对于红色方框中的像素,假设其中有些像素对应的梯度方向落在 0 到 20 区间,那么将这些像素对应的梯度幅值在 0 到 20 区间内进行累加,同理其他区间也做同样的运算,最终得到下图中右边的方向梯度直方图。同样地,整张图片中的所有 Cells 都用同样的方法计算方向梯度直方图。
区域(Blocks)归一化
我们已经将图像分成若干个 Cells,并且计算了每个 Cell 的方向梯度直方图。接下来我们要对图像进行区域归一化处理,归一化的目的是减少光照变化对图像梯度的影响。 现在让我们来看看如何进行归一化处理。
首先我们先来介绍什么是区域(Blocks),为避免歧义下文皆书写为 Block 或 Blocks,前面我们将图像分成若干个 Cells,每个 Cell 内有若干个像素,类似地,一个 Block 是一块由若干个 Cells 组成的矩形。对图像进行归一化的过程类似于前面实验学习的滑动窗口,将一个 Block 从左向右、从上向下在图中滑动,然后在每个 Block 区域内进行归一化计算。
让我们通过下图来理解如何通过 Blocks 对图片进行归一化。 下图中右边图片是我们从原图片中选取的一部分,在这块区域里面有若干个 Cells,我们用红色矩形框表示一个 Blcok,红色矩形框在图上向右滑动一个 Cell 的步长后我们就得到了蓝色矩形框,所以区域归一化的方法就是设定一个尺寸为 $K\times K$ 个 Cells 的 Block,在图上从左向右、从上向下滑动,然后在每个 Block 内进行归一化。

在每个 Block 内有 $2\times 2$ 个 Cells,前面我们将梯度方向分为 9 个区间并为每个 Cell 计算了方向梯度直方图,故每个 Cell 有 9 个向量,则在一个 Block 内共有 $2\times 2\times 9$ 个向量。然后我们可以使用 $L1$ 范数或 $L2$ 范数对 Block 内的向量进行归一化。其中使用 $L2$ 范数进行归一化的效果相对较好,下面就是使用 $L2$ 范数归一化的公式,即 Block 内的每个向量除以由 Block 内所有向量计算得到的 $L2$ 范数。其中 $v_i$ 表示 Block 内的向量,$\epsilon$ 的作用是防止出现分母为 0 的情况,它是一个很小的值。
$$ v = \frac{v_i}{\sqrt{\sum_{i=1}^n{v_i^2} + \epsilon^2}} $$
从上图中可以看出每一个 Cell 不止出现在一个 Block 内,也就是说一个 Cell 将被重复的用于归一化计算中,这样做会看似比较冗余,但是会提高特征描述的表现。最后对所有的 Block 完成归一化计算,合并所有获得的归一化后的向量,这样我们就完成了图像的 HOG 特征化表示。
使用 Scikit-image 实现方向梯度直方图
以上所述的概念或公式也许没法在短时间内理解消化,不过也不用太过担心,因为 HOG 已经在现有的一些算法库中实现,所以我们完全不用花时间再去复现它。
可以使用 feature.hog 用于计算图片的方向梯度直方图。该函数的参数意义如下所示。
- 第一个参数
image表示输入图像。 orientations表示要将梯度方向分成几个区间,这里我们将梯度方向分为 9 个区间。pixels_per_cell表示 Cell 的尺寸,即一个 Cell 中有几个像素,需要传递一个元组给该参数,我们将(8, 8)传递给该参数。cells_per_block表示每个 Block 的尺寸,即一个 Block 中有几个 Cells,这里需要传递一个元组给该参数,我们将(2, 2)传递给该参数。transform_sqrt表示伽马校正,我们将True传递给该参数表示使用伽马校正预先对图片进行归一化处理。visualize表示可视化,将True传递给该参数表示返回 HOG 图像。
from skimage import feature |

