人工神经网络

传统的算法需要花费大量时间人为的设计特征，在实际应用中面对复杂的背景和目标时往往表现得并不理想。但是随着深度学习的崛起目标检测的性能和表现得到了大幅度的提升，深度学习的发展推动了目标检测的迅猛发展。

深度学习是人工智能的一个分支，其受人脑的结构和功能的启发，通过人工神经网络（Artificial Neural Network）模仿人脑处理数据和决策的方式从数据中学习内在规律和特征表示。随着近年的计算机性能的发展和海量数据的增长使得深度学习成为机器学习中的热门研究方向。如今深度学习已经广泛应用于我们的日常生活中，如在线翻译、人脸识别、语音转换等。

人工神经网络（Artificial Neural Network）是一类可以从提供的数据中学习的机器学习算法，是一种模仿人脑神经系统处理信息的运算模型，其由大量的节点或称为神经元相互连接构成。一个节点由输入（Input)、权重（Weight)、偏差（Bias）、激活函数（Activation Function）、输出（Output）组成。下图左边的图片是一个简单的三层神经网络，其中每一个圆形表示一个节点且每一个节点都与下一层中的每个节点相连接。黄色节点所在的层被称为输入层（Input Layer），绿色节点所在的层被称为输出层（Output Layer），在神经网络中除去输入层和输出层的部分被称为隐藏层（Hidden Layer）。

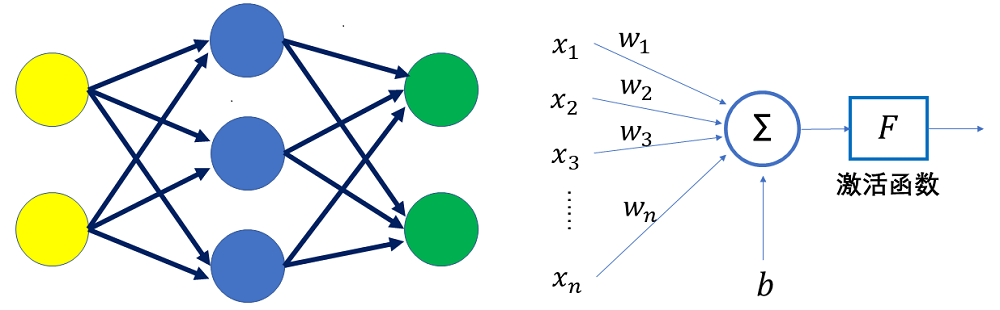
上图右边的图片是一个节点或称为神经元，$x_1, x_2, x_3 … x_n$ 表神经元的输入（这些 $x$ 可以是像素值、语音、文字等），每一个 $x$ 都有一个与之对应的权重 $w$。这些权重值在训练过程中会被不断地更新，拥有较高权重值的 $x$ 会被认为是比较重要的信息， 反之拥有较低权重值的信息会被认为不太重要。$b$ 表示偏差。我们将 $x$ 和 $w$ 相乘再求和，将求和结果加上偏差后输入一个激活函数得出最后的输出。这就是一个感知器的典型结构。将计算过程用数学方式来表达就是下面的公式。

$$y = f(x_1w_1 + x_2w_2 + x_3w_3 + … + x_nw_n + b) \quad 或 \ y = f(\sum_{i=1}^nx_iw_i + b)$$

激活函数（Activation Function)

激活函数为人工神经网络处理非线性问题提供了重要作用，其引入了非线性因素并且为节点建立一个输出边界，激活函数增加了神经网络的复杂性和网络学习复杂事物的能力。常见的激活函数有 Step、Sigmoid、Tanh、ReLU、Leaky ReLU、ELU，这里我们将向大家介绍 Sigmoid 函数。

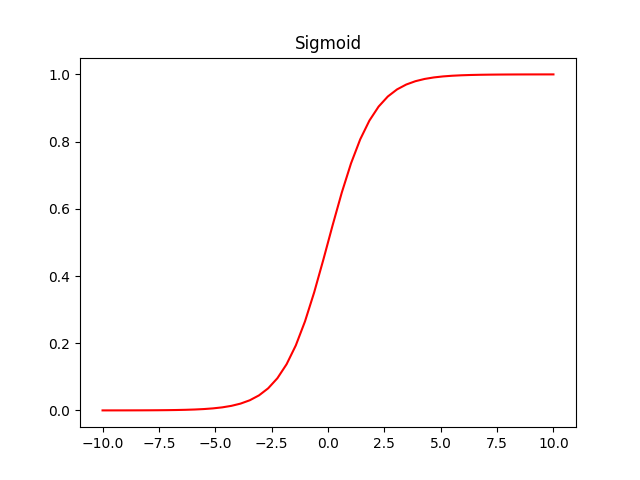
Sigmoid 函数是神经网络中一个常见的激活函数。下面是 sigmoid 公式，其中 $x$ 是上面求和的结果 $y$。

$$s(x) = \frac{1}{1 + e^{-x}}$$

下图是 Sigmoid 函数图，它的值在 0 到 1 之间。可以看到 $x$ 越小 $y$ 越接近 0，反之 $x$ 越大 $y$ 越接近 1。Sigmoid 函数曾被大量使用，但是由于其会导致梯度反向传递时，梯度爆炸和梯度消失，近年来使用越来越少。

前馈神经网络（Feed Forward Network）

前馈神经网络或前馈网络是深度学习中常见的一种单向网络，每一层的神经元只接收前一层神经元的输出并将自身的输出传递给下一层的神经元。信息从输入层逐层传递最后从输出层输出结果，整个网络没有反馈和中间跳转层。

反向传播（Back Propagation）

在使用神经网络解决问题时，信息经过神经网络的前向传播最后得出的结果会与期望的结果有偏差，这时我们需要计算实际输出结果和期望结果之间的误差，并将该误差反向地从输出层向输入层传播，以此来更新权重以达到优化神经网络的目的，这个过程就是神经网络训练的过程。

首先为了实现反向传播，激活函数必须是可微分的，然后我们计算误差 $error$ 对 $w^l_{j,k}$ 的偏导数，$w^l_{j,k}$ 表示从 $(l-1)^{th}$ 层的第 $k$ 个节点到 $l^{th}$ 层的第 $j$ 个节点上的权重。下面是求偏导数的公式，其中 $\partial o_k$ 表示当前层第 $k$ 个节点的输出，$\partial net_k$ 表示当前层第 $k$ 个节点的输入。

$$\frac {\partial error} {\partial {w^l_{j,k}}} = \frac {\partial error} {\partial o_k} \frac {\partial o_k}{\partial net_k} \frac {\partial net_k}{\partial w^l_{j,k}}$$

至此，我们已经学习了神经网络的基本结构和原理。看了上面的公式大家也许依然无法理解反向传播的计算方法，但是不用担心，在下一节中我们将会使用代码构建一个简单的神经网络，这样能够帮助大家很好的理解神经网络的结构和原理。

代码实现

下面简单的构建一个神经网络，首先导入 NumPy 模块。然后我们设定一个学习率 alpha 用于控制网络的学习进度，这里我们设定一个值为 0.1。

import numpy as np
alpha = 0.1

然后我们创建一个 set_w 函数对神经网络进行一些初始化处理。该函数有一个输入值 layers，这个输入值是一个列表，表示网络的结构，例如我们给函数输入一个列表 [3, 2, 1] 表示这个网络的输入层有 3 个节点，隐藏层有两个节点，输出层有 1 个节点。

def set_w(layers):
    W = [np.random.randn(x + 1, y + 1) / np.sqrt(x)
        for x, y in zip(layers[:-1], layers[1:-1])]
    
    w = np.random.randn(layers[-2] + 1, layers[-1])
    W.append(w / np.sqrt(layers[-2]))
    
    print("Network Layers: {}".format("-".join(str(n) for n in layers)))
    return W

上面代码第 2、3 行表示我们创建一个 W 列表用于存储从 $(l-1)^{th}$ 层到 $l^{th}$ 层的权重。首先通过 zip(layers[:-1, layers[1:-1]) 分别获取 $(l-1)^{th}$ 层和 $l^{th}$ 层（这里不包括最后一层）的节点数 x 和 y，然后使用 np.random.randn 随机初始化一个标准正态分布的矩阵 $(x+1) \times (y+1)$，这里 x + 1 和 y + 1 表示我们在每层添加了一个偏置值，最后除以 x 的开方来标准化每个节点的输出。 例如我们网络结构是 [4, 3, 2, 1]，则第一层到第二层的权重矩阵是 $4 \times 3$，但是我们又在每层添加了一个偏置值，则权重矩阵变为 $5 \times 4$，这样处理的好处是将偏置值和权重一起训练而不用手动调参。

上面第五行代码类似第 2、3 行代码，表示生成一个 w 矩阵，矩阵的行数是网络倒数第二层的节点数加一个偏置值，列数是最后一层节点数（因为最后一层是输出层，故这里就不用添加偏置值）。

上面第 6 行代码表示使用倒数第二层的节点数的开方对 w 进行标准化，然后将其添加到 W 中，最后第 8 行输出每层节点数。

下面我们构建一个 sigmoid 激活函数，该函数需要一个输入值 x。在函数内我们根据前面提到的激活函数公式计算激活值并返回计算结果。

def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

接下来我们构建一个 sigmoid_deriv 函数，该函数同样需要一个输入值 x。在函数内我们计算 sigmoid 函数的导数并返回计算结果。

def sigmoid_deriv(x):
    return x * (1 - x)

下面我们构建一个 feedforward 函数，该函数需要一个输入值 data, 这个 data 表示输入网络的数据集。我们使用这个函数实现前向传播，当训练完神经网络，我们将使用这个函数进行结果预测。在函数内首先使用 np.atleast_2d 确保 data 至少是 2 维数组。因为我们将偏置添加进了权重矩阵，所以在第三行代码中我们使用 np.c_ 在数组的每一行的末尾添加一个 1。

代码的第 5、6 行表示我们用 for 获取 W 中每个权重矩阵，然后分别使用矩阵乘法和 sigmoid 函数对数据进行预测。最后返回预测值。

def feedforward(data):
    p = np.atleast_2d(data)
    p = np.c_[p, np.ones(p.shape[0])]
    
    for layer in np.arange(0, len(W)):
        p = sigmoid(np.dot(p, W[layer]))
        
    return p

下面我们创建一个 loss 函数用于计算实际输出结果和期望结果之间的误差。该函数有两个输入值，data 数据集和数据集中每个数据对应的标签。在函数内我们首先使用 np.atleast_2d 确保 data 至少是 2 维数组，然后使用 feedforward 函数计算数据集的预测结果 predictions。最后我们计算预测结果与真实标签的误差 loss。

def loss(data, y):
    y = np.atleast_2d(y)
    predictions = feedforward(data)
    loss = 0.5 * np.sum((predictions - y) ** 2)

    return loss

接下来我们将创建一个 backprop 函数， 这个函数将用于计算反向传播。该函数需要两个输入值 x 和 y 分别表示数据集中的每个数据和其对应的标签。下面的第 2 至 7 行代码与 feedforward 函数类似这里就不多赘述了，第 8 行代码先将网络的每层矩阵相乘结果作为 sigmoid 函数的输入，然后将函数计算结果添加到列表 A 中。

第 10 行代码开始就是反向传播的过程，首先计算网络的输出值与标签值的差，这一步其实是loss 函数的导数。第 11 行代码我们创建一个列表 D 用于存储梯度变化的量,根据链式法则计算 error 与 sigmoid 函数的导数的乘积。列表中的值将用于更新权重矩阵。

def backprop(x, y):
    a = np.atleast_2d(x)
    A = [np.c_[a, np.ones((a.shape[0]))]]

    for layer in np.arange(0, len(W)):
        
        out = sigmoid(A[layer].dot(W[layer]))
        A.append(out) 

    error = A[-1] - y
    D = [error * sigmoid_deriv(A[-1])]

    for layer in np.arange(len(A) - 2, 0, -1):
        delta = D[-1].dot(W[layer].T)
        delta = delta * sigmoid_deriv(A[layer])
        D.append(delta)
 
    D = D[::-1]

    for layer in np.arange(0, len(W)):
        W[layer] += -alpha * A[layer].T.dot(D[layer])

第 13 到 16 行计算每层的梯度变化量，我们使用 for 循环反向遍历网络的每一层（不包括最后一层，因为最后一层网络的梯度变化我们已经在第 11 行计算了）。第 14、15 行计算当前层的梯度变化 delta, delta 就等于前一层的梯度变化 D[-1] 与当前层的权重的转置矩阵相乘，然后再与当前层的 sigmoid 函数的导数相乘。第 16 行将计算后得到的 delta 添加到列表 D 中。

上面第 18 到 21 行将更新权重矩阵。第 18 行将颠倒 D 中 delta 的顺序，因为 delta 是通过反向传播从输出层向输入层计算的，所以在更新权重矩阵时要将其顺序颠倒。第 20、21 行使用 for 循环遍历网络的每一层，在每一层我们将当前层的激活函数的转置矩阵和 D 中的 delta 相乘，再乘以负的学习率 alpha，最后我将计算得到的值与当前层的权重相加即可完成权重的更新。

下面是创建一个 train 函数用于训练网络。该函数需要 3 个输入值，data 表示输入的数据集，y 是每个数据的标签，epochs 表示训练的次数，这里我们设置一个默认值 500。

def train(data, y, epochs = 500):
    for epoch in np.arange(0, epochs):
        for (x, label) in zip(data, y):
            backprop(x, label)

        print("epoch: {}, loss: {}".format(epoch + 1, loss(data, y)))

在函数内首先使用一个 for 循环用于执行 epochs 次训练。接下来使用一个 for 循环获取 data 和 y 中的每个数据 x 和其对应的标签 label，在循环内我们执行 backprop 函数,将获取的数据和标签作为函数的输入值。最后输出每次训练后的误差。至此神经网络已经构建完成了。