卷积神经网络

介绍

在之前的文章中，我们了解到神经网络的输入层中的每个节点都与下一层的每个节点相连接，我们称这种连接方式为全连接（Fully-connected），但是这种全连接方式存在一些明显的缺陷。首先如果使用全连接网络处理图片的话，需要将图像矩阵转换为一列向量，这样就破坏了图像的空间信息。其次假设我们将一张尺寸为 $240\times240\times3$ 的三通道图片作为全连接网络的输入，则在输入层总共需要 172800个权重，如此多的参数需要很大的计算量和时间处理，并且大量的参数还会导致过拟合（模型在训练集上表现好，在测试集上表现差，泛化能力差）。在计算机视觉中广泛应用的卷积神经网络可以用来克服上述问题，在卷积神经网络中我们采取局部连接节点的方式代替全连接的方式，通常一个卷积神经网络由输入层、卷积层，激活层、池化层和全连接层构成。

卷积和卷积核

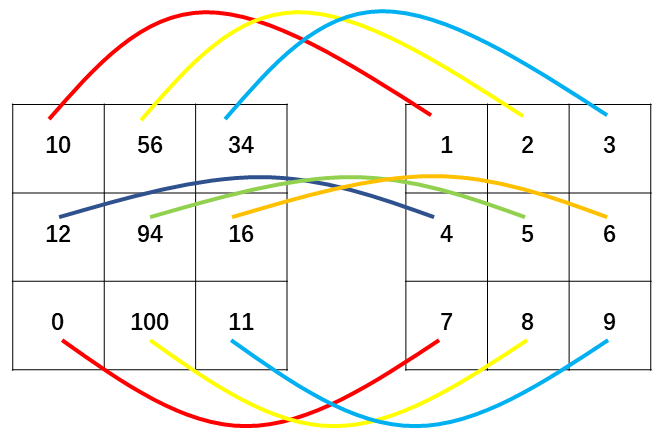
在开始学习卷积神经网络前，我们需要了解卷积和卷积核（Kernel）的相关内容。通常情况下，深度学习中所谓的卷积实际上是互相关操作（在后面的内容中我将用卷积来称呼互相关操作），如下图，两个矩阵的卷积即是将两个矩阵中对应位置的元素相乘再求和，则这两个矩阵的卷积结果是 $10\times1 + 56\times2 + 34\times3 + 12\times4 + 94\times5 + 16\times6 + 0\times7 + 100\times8 + 11\times9 = 1737$。

现在让我们来了解下图片的卷积是如何操作的，在图片上进行卷积需要用到卷积核（kernel），卷积核实际上就是一个矩阵，我们让这个矩阵在图像上从左向右、从上向下滑动，在滑动的过程中矩阵所覆盖的区域内的像素值与矩阵内元素按位相乘再求和，这些求和结果组成一个新的矩阵我们称之为特征图（Feature map）。

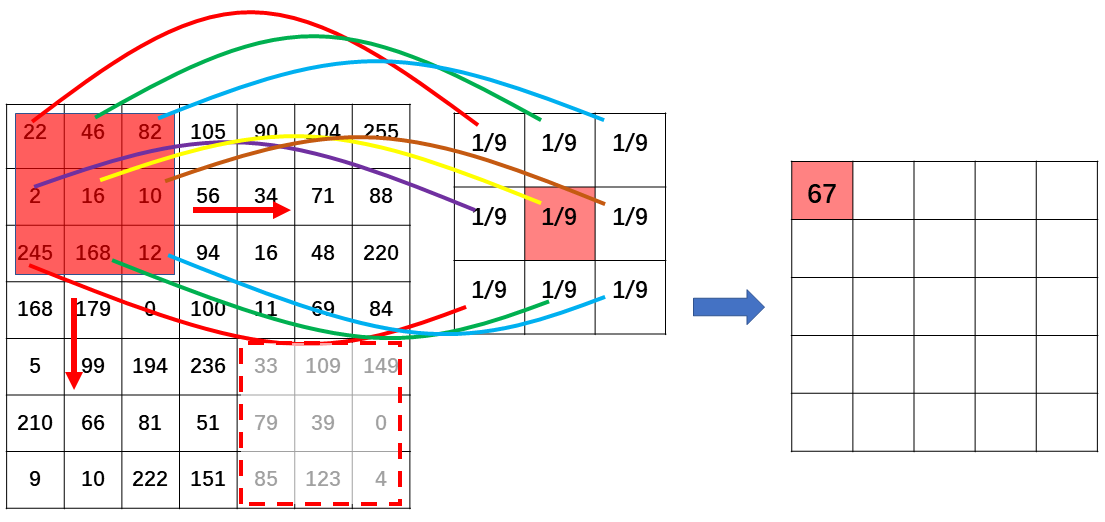
这个过程类似我们学习过的滑动窗口，假设我们使用一个 $3\times3$ 的卷积核（下图中间的矩阵，矩阵中每个值都为 1/9）对一张 $7\times7$ 尺寸的图片进行卷积，那么首先将卷积核的左上角顶点与图片的左上角顶点重叠，下图左边矩阵上的红色区域为重叠区域，然后按位计算红色矩形区域的元素与卷积核中的元素的乘积再将所有乘积结果求和，就得到了特征图上的第一个值为 67，然后按照从左向右、从上向下的顺序依次移动 1 个像素的距离（每次移动的像素个数称为步长（Stride），也可以移动多个像素）然后再计算重叠部分的卷积直到卷积核到达图片的左下角（下图左边矩阵的左下角虚线框），这样我们就获得了一个 $5\times5$ 的特征图。需要注意的是卷积核的尺寸必须是奇数，例如 $1\times1$、$3\times3$、$5\times5$ 等。

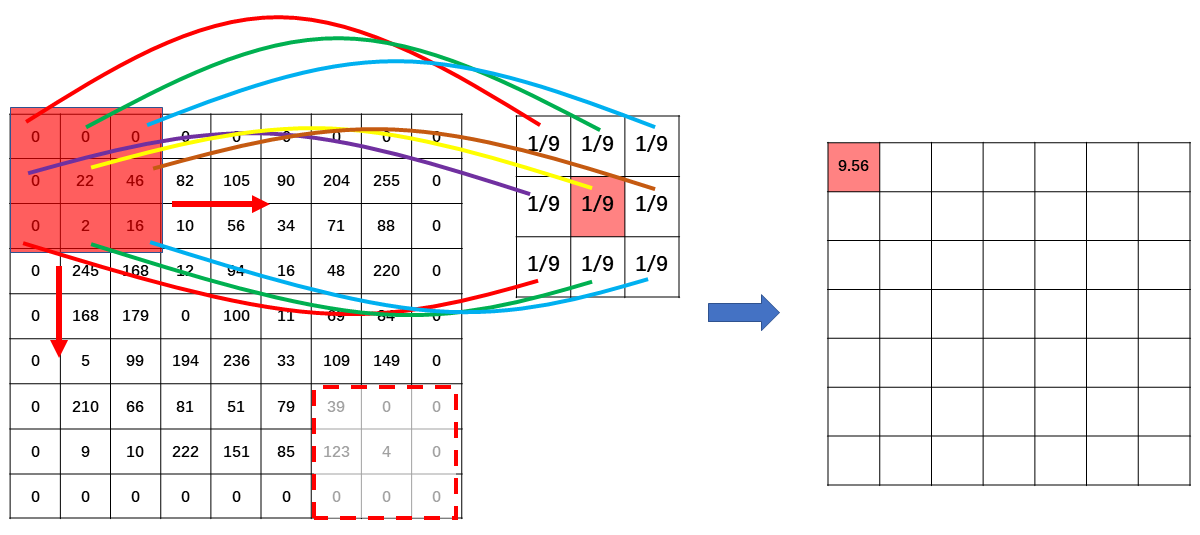
使用上述卷积方法得到的特征图尺寸会缩小，同时会丢失图片的边缘信息，因为卷积核移动到图片的边缘就结束了。为了解决这个问题，我们可以使用填充（Padding）方法，填充就是在图片外围填充像素值为 0 的像素点（见下图最左边矩阵），然后通过卷积计算得到的特征图尺寸就和输入图片的尺寸一样了。填充不仅可以在卷积过程中保留图像边缘信息，还可以对不同尺寸的图片进行填充，统一图片尺寸。

卷积层

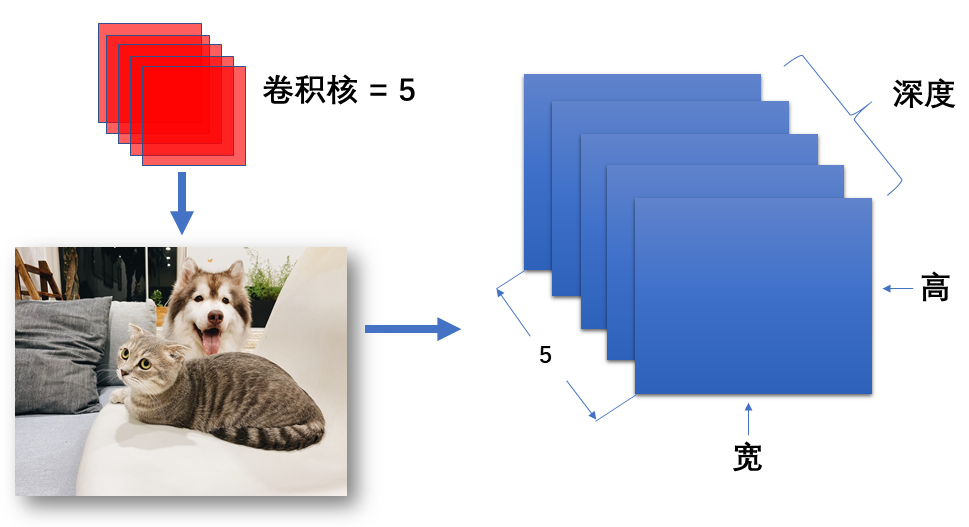
卷积层是卷积神经网络的最重要组成部分，卷积层就是由不同数量和尺寸的卷积核构成的，其作用是用于图像的局部特征提取。在卷积神经网络中我们经常会遇到一个概念称为深度（Depth），深度与图像的通道类似，我们使用一个卷积核对图像进行卷积操作后会得到一个二维特征图，这个特征图和输入图像一样具有高和宽，使用多个尺寸相同的卷积核对输入图像进行卷积时我们将得到多个特征图，将这些特征图堆叠起来将得到一个三维特征图，这三个维度分别对应宽、高和深度，深度值就等于卷积核的个数。

如下图，我们使用 5 个尺寸相同的卷积核对图像进行卷积，我们将得到 5 个特征图，将这 5 个特征图堆叠起来就是一个具有宽、高和深度的三维矩阵，这个矩阵的深度就是 5。提到深度我们还需要了解一个概念称为滤波器（Filter），滤波器是由多个卷积核堆叠而成，其深度是其内卷积核的数量，当卷积核的个数为 1 时可以认为滤波器等同于卷积核。当给网络输入一张 RGB 图片时，由于图片有三个通道，需要用三个卷积核对图片进行卷积，这三个卷积核就构成一个滤波器。

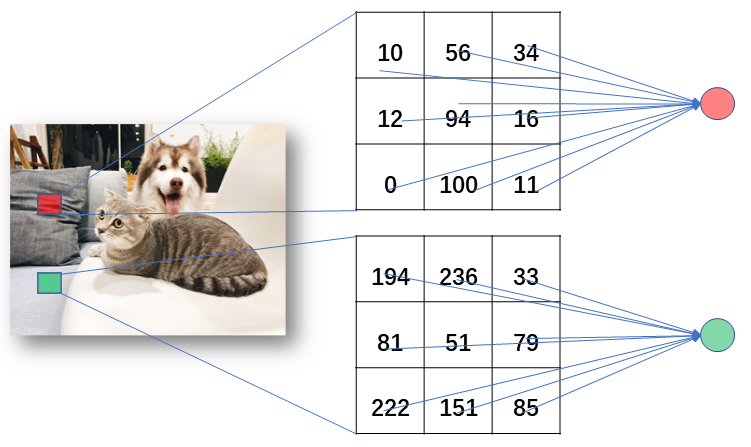
在卷积神经网络中我们采取局部连接节点的方式代替全连接的方式，如下图，右边两个圆表示神经元节点，每个节点只与图片上的部分区域的像素值（下图中间的矩阵表示局部像素点）连接，这些区域之外的其他像素值都不会影响与这个区域相连的节点，这些区域称为对应节点的感受野（Receptive field）。如果输入网络的图像尺寸是 $16\times16\times3$（图像的宽、高是 16，通道数是 3），假设感受野的尺寸是 $3\times3$ 那么每个与这个区域连接的节点将接受 $3\times3\times3 = 27$ 个权重（图像有三个通道）。假设我们输入的尺寸是 $5\times5\times100$ 以及感受野是 $3\times3$，则与之相连的节点所接受的权重个数是 $3\times3\times100 = 900$ 。

激活层

激活层在每一个卷积层后，其作用是引入了非线性因素为节点建立一个输出边界，判断各区域特征强弱来筛选有用特征。例如通过卷积后的一块区域没能达到激活阈值，则激活函数将输出 0，表示这块区域提取的特征无关紧要。在卷积神经网络中比较常用的是 ReLU 函数，在本节实验我们并不需要了解 ReLU 函数的公式，因为现有的开源框架中已经内置了一些激活函数，我们只需要调用就行了。

池化层

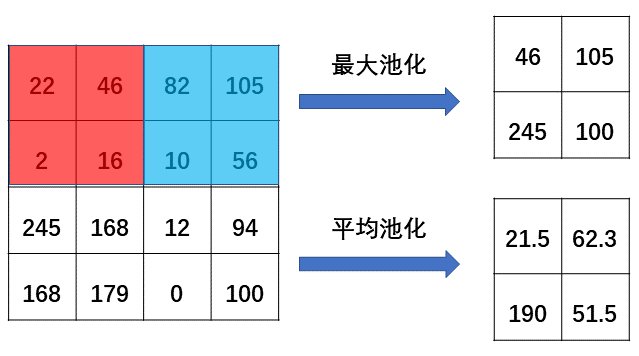
池化（Pooling）最直观的作用就是压缩输入的尺寸（当卷积核的步长大于 1 时也可以压缩输入尺寸），池化层通常放在激活层之后。池化方法有两种，最大池化（Max pooling）和平均池化（Average pooling）。最大池化就是选定域内最大值来表示该区域，下图中我们在 $4\times4$ 的矩阵中选定 $2\times2$ 区域进行池化，选出这个区域内最大值 46 来表示该区域，然后向左移动 2 个步长，在新的区域中选择最大值 105 来表示该区域，依次类推我们将原来的 $4\times4$ 矩阵压缩到 $2\times2$ 尺寸。同理平均池化就是选定区域内的平均值表示该区域。

全连接层

全连接层就是前一层的激活值与这一层所有的节点相连

Dropout

在全连接层后我们通常会进行 Dropout 操作，Dropout 是一种预防过拟合提高模型准确率的方法。其原理是在训练过程中以一定概率随机丢弃部分节点从而提高模型的泛化能力