数组在计算机中是以连续空间的形态存在，而链表则是不要求空间连续，每一个元素都保存着下一个元素的地址，使其更加灵活。

约瑟夫环问题

问题描述

著名的约瑟夫问题：编号为 1-N 的 N 个士兵围坐在一起形成一个圆圈，从编号为 1 的士兵开始依次报数（1，2，3… 这样依次报数），数到 m 的 士兵会被淘汰出列，之后的士兵再从 1 开始报数。直到最后剩下一个士兵，求这个士兵的编号。

求解思路

假设我们现在需要使用数组解决该问题，用一个数组存在 1，2，3，4，5 … 编号，要求返回最后一个士兵的编号。思路如下

  • 初始化剩下的士兵人数 retainNum 为 n，循环下面的操作，直到全部士兵出圈。
  • 初始化 k = 0，从第一个士兵开始计数，每次遍历到数值不为 -1 的元素，则 k+1，如果 k = M，则说明该士兵需要被淘汰出局，则元素的值置为 -1，淘汰的数量 num + 1，且 k 重新赋值为 0。
  • 遍历数组元素，找到数值不为 -1 的元素，就是最后剩下的士兵。

假设 5 个士兵，数到 3 就淘汰，具体的执行过程如下：

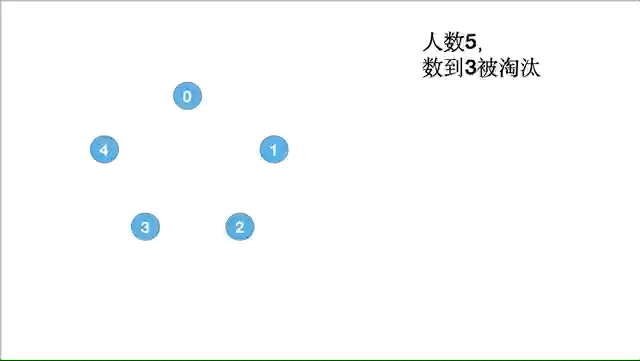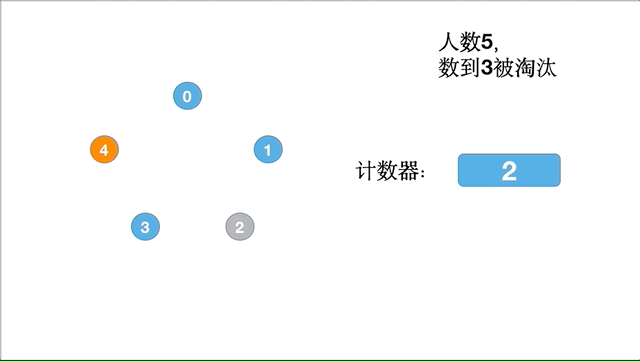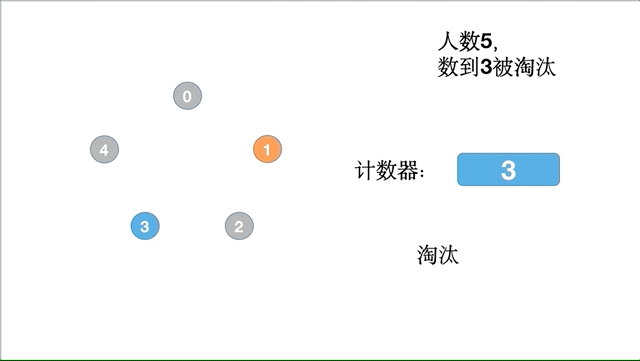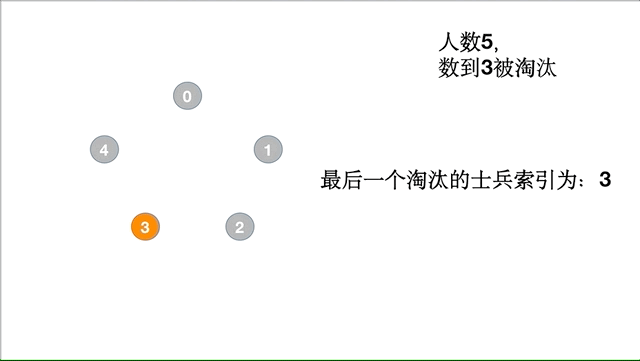
代码实现如下：

/**
 * @param {number} n
 * @param {number} m
 * @return {number}
 */
var lastRemaining = function(n, m) {
    let peoples = new Array(n);
    // 当前指针索引
    let index = -1;
    // 循环数 0 到 m
    let count = 0;
    // 环中剩下的人数
    let remainNum = n;
    // 将所有的人数都淘汰出圈
    while (remainNum > 0) {
      // 索引 +1
      index++;
      // 如果当前索引已经超过数组的长度，则需要将索引移动至数组的开头位置
      if (index == n) {
        // 索引移动至开头
        index = 0;
      }
      // 如果元素的值等于 -1，说明这个士兵已经被淘汰了，不计数，直接跳过
      if (peoples[index] == -1) {
        continue;
      } else {
        // 否则计数
        count++;
        // 如果计数到 m，说明该士兵需要被淘汰
        if (count == m) {
          // 数值置为 -1
          peoples[index] = -1;
          // 计数归 0
          count = 0;
          // 圈内的人数减少 1
          remainNum--;
        }
      }
    }
    return index;
};

滑动窗口的最大值

问题描述

假设给定一个整形数组 nums 和一个大小为 k 的窗口，k 小于 nums 的长度，窗口从数组的最左边，每次滑动一个数，一直到最右边，返回每次滑动窗口中的最大值的数组。

假设输入的数组为 nums[] = { 3， 5 ， -1 ， 3 ， 2 ， 5 ， 1 ， 6 }，窗口大小 k = 3。

滑动窗口具体如下，[] 中即滑动窗口的内容

[ 3  5  -1]  3  2  5  1  6       5
  3 [5  -1   3] 2  5  1  6       5
  3  5 [-1   3  2] 5  1  6       3
  3  5  -1 [ 3  2  5] 1  6       5
  3  5  -1   3 [2  5  1] 6       5
  3  5  -1   3  2 [5  1  6]      6

求解思路

  • 遍历数组 nums[] 中的元素 num[i]，执行以下的操作。
  • 执行循环：如果队列不为空，且以队列的最后一个元素为下标的数组元素 nums[queue.peekLast()] 小于 num[i] 时，将队列的最后一个元素删除。意为：删除队列中较小的元素索引。
  • 将当前元素下标 i 添加到队列的尾部。
  • 如果队列的队首元素小于 i-k，则移除队首的元素，说明队首的元素索引已经超过了滑动窗口的长度了，应该抛弃队首的索引。
  • 如果 i 大于等于 k-1，那么说明滑动窗口长度已经生效，此时的队列第一个元素作为索引，取出数组中的数值，就是 i-k+1 为起始的滑动窗口的最大值。

以 nums[] = {3，5，-1，3，2，5，1，6} 为例，窗口大小 k = 3。

  • i = 0，nums[0] = 3，队列为空，添加索引 0 到队列尾部，队列为 { 0 }。

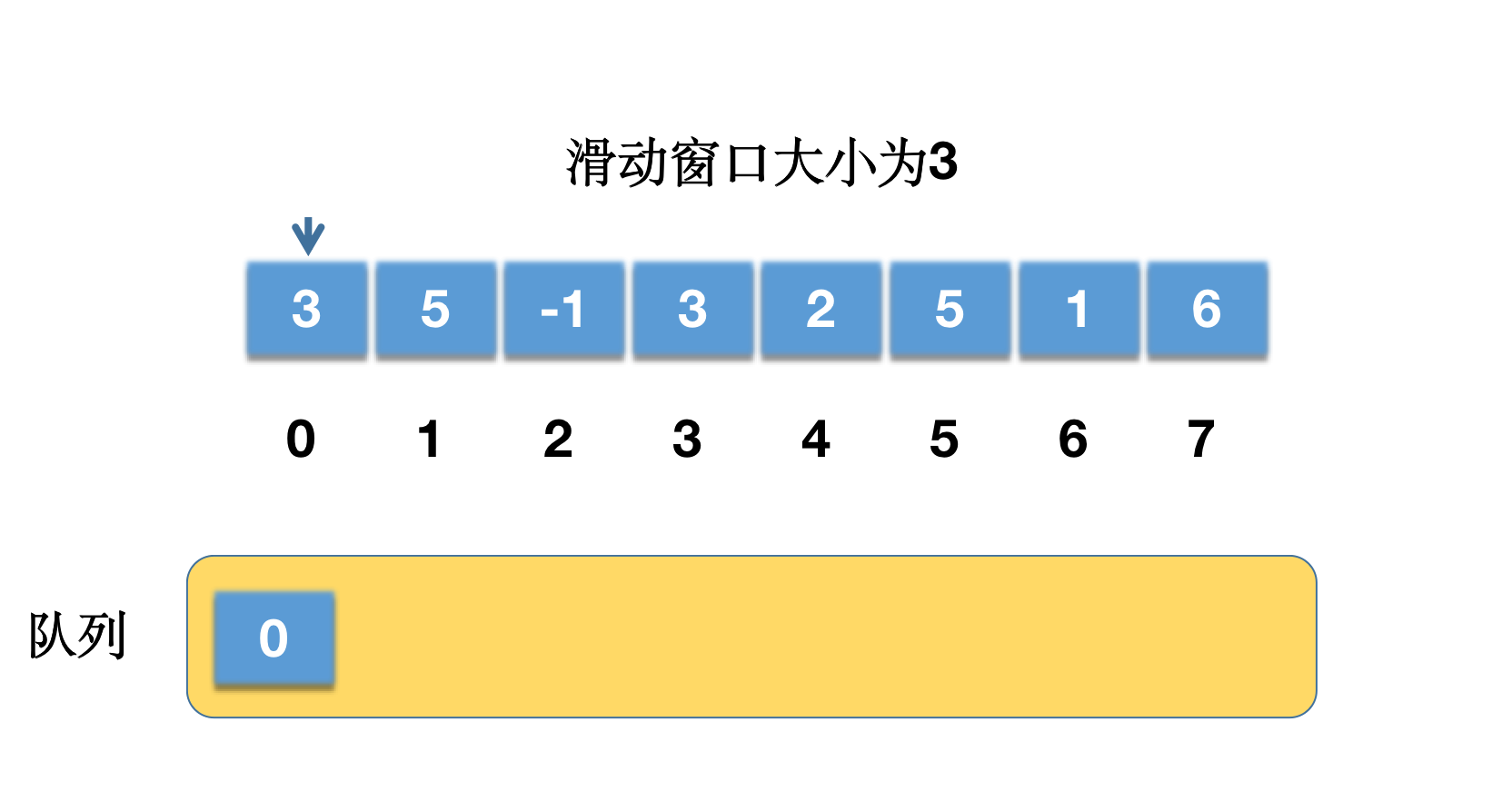
  • i = 1，nums[1] = 5，队列为 { 0 }，队列尾部元素为 0，nums[0] < nums[1]，则需要把 0 移除，此时队列为 {}，添加 1 进去，队列变为 { 1 }。

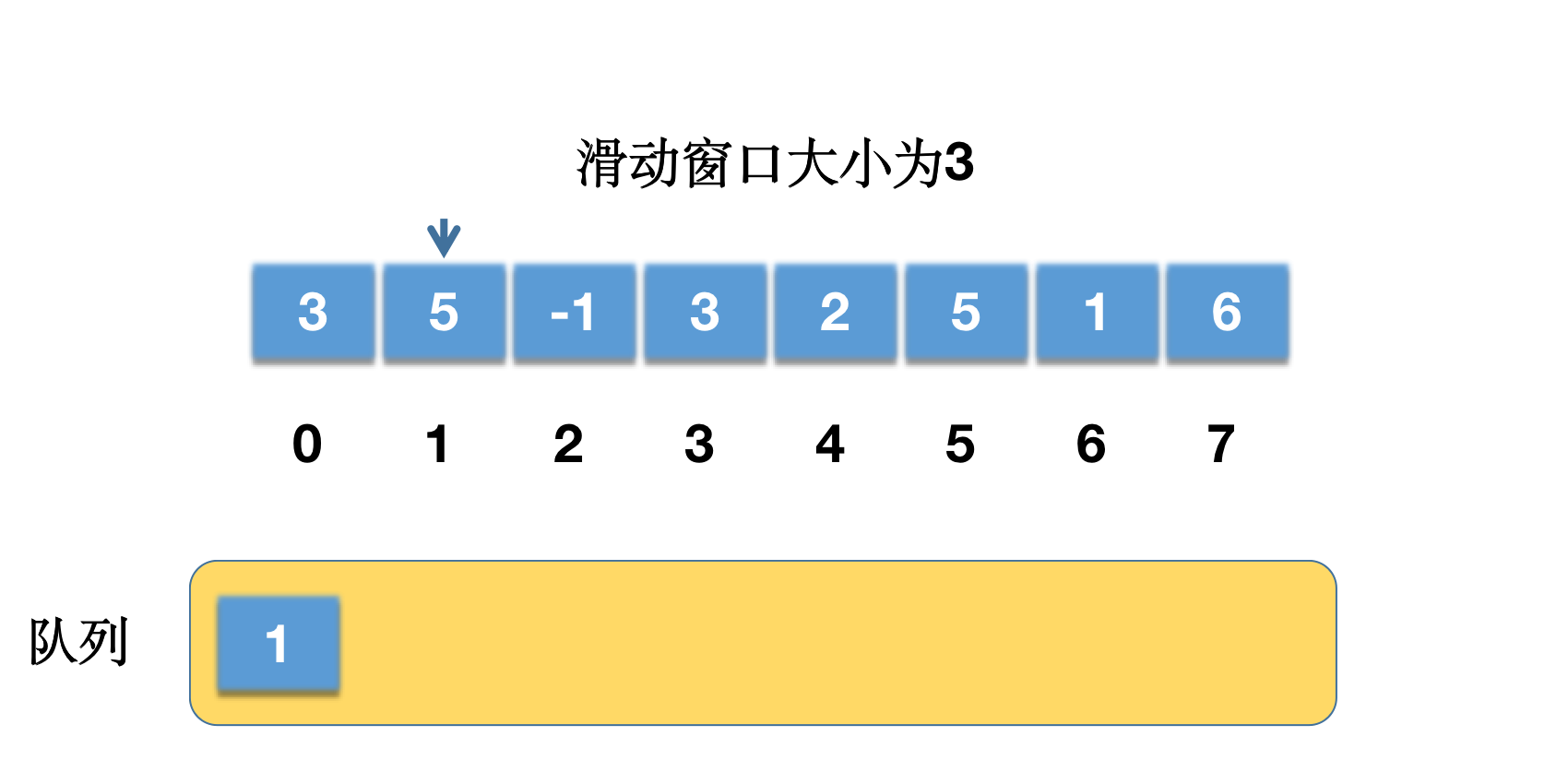
  • i = 2，nums[2] = -1，队列为 {1}，队列尾部元素为 1，nums[1] > nums[2]，不移除，直接把索引 2 加到队列中，队列变成 { 1，2 }，此时 i >= k-1 满足，也就是滑动窗口生效。results[i-k+1] = results[0] 的值为以队列的第一个元素 1 为索引的数组元素，即 nums[1] = 5，因此 results[0] = 5。

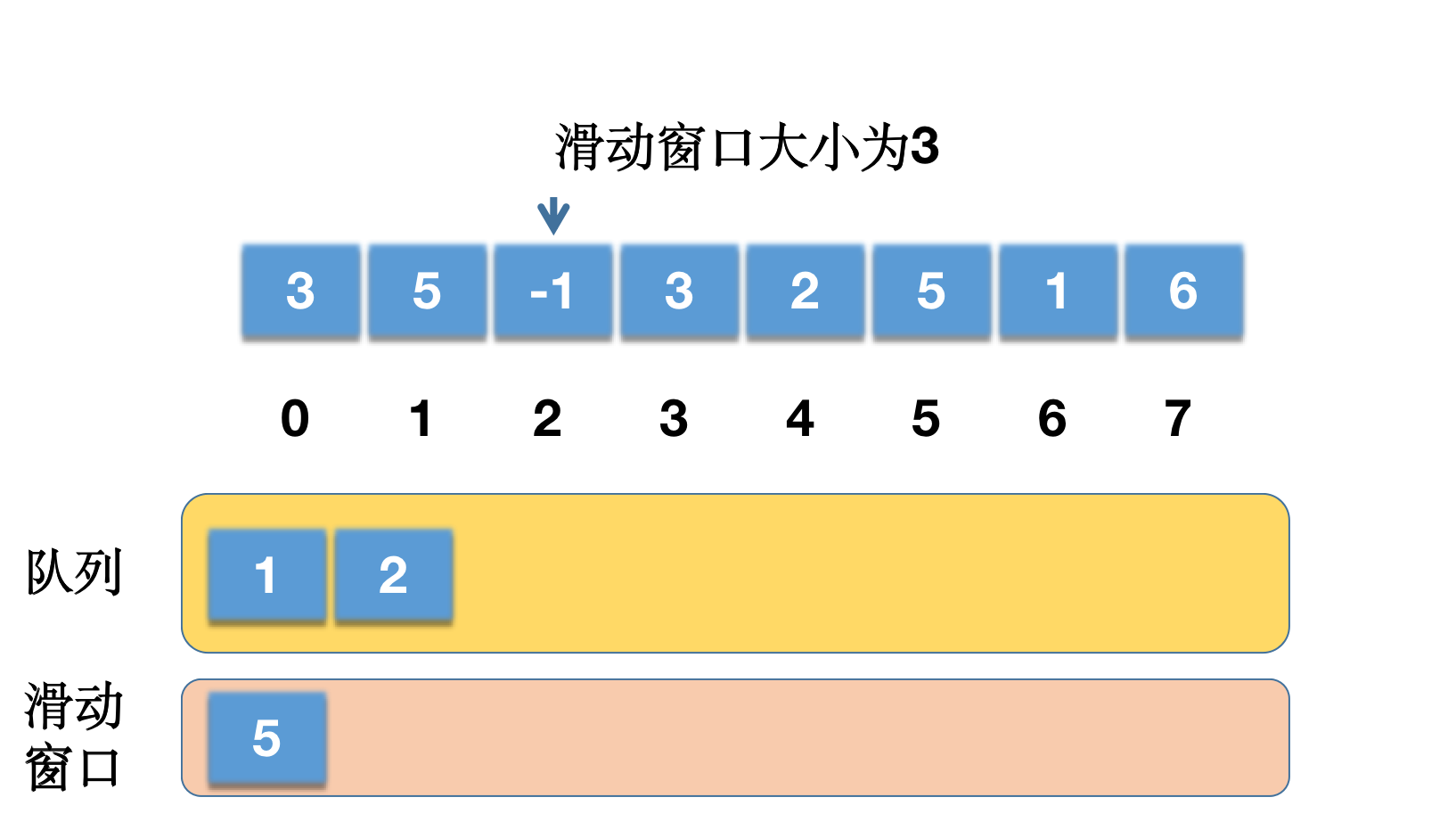
  • i = 3，nums[3] = 3，此时队列为 { 1，2 }，队列尾部元素为 2，nums[2] < nums[3]，因此需要将队列尾部的 2 移除，队列变成 { 1 }，此时队尾元素为 1，nums[1] = 5 > nums[3]，不再移除元素。将当前的索引 3 添加至队列中，队列变成 { 1，3 }。此时的队首元素的为 1，当前遍历索引为 3，符合条件，不做移除，results[i-k+1] = results[1] 的值为以队列的第一个元素 1 为索引的数组元素，即 nums[1] = 5，因此 results[1] = 5。

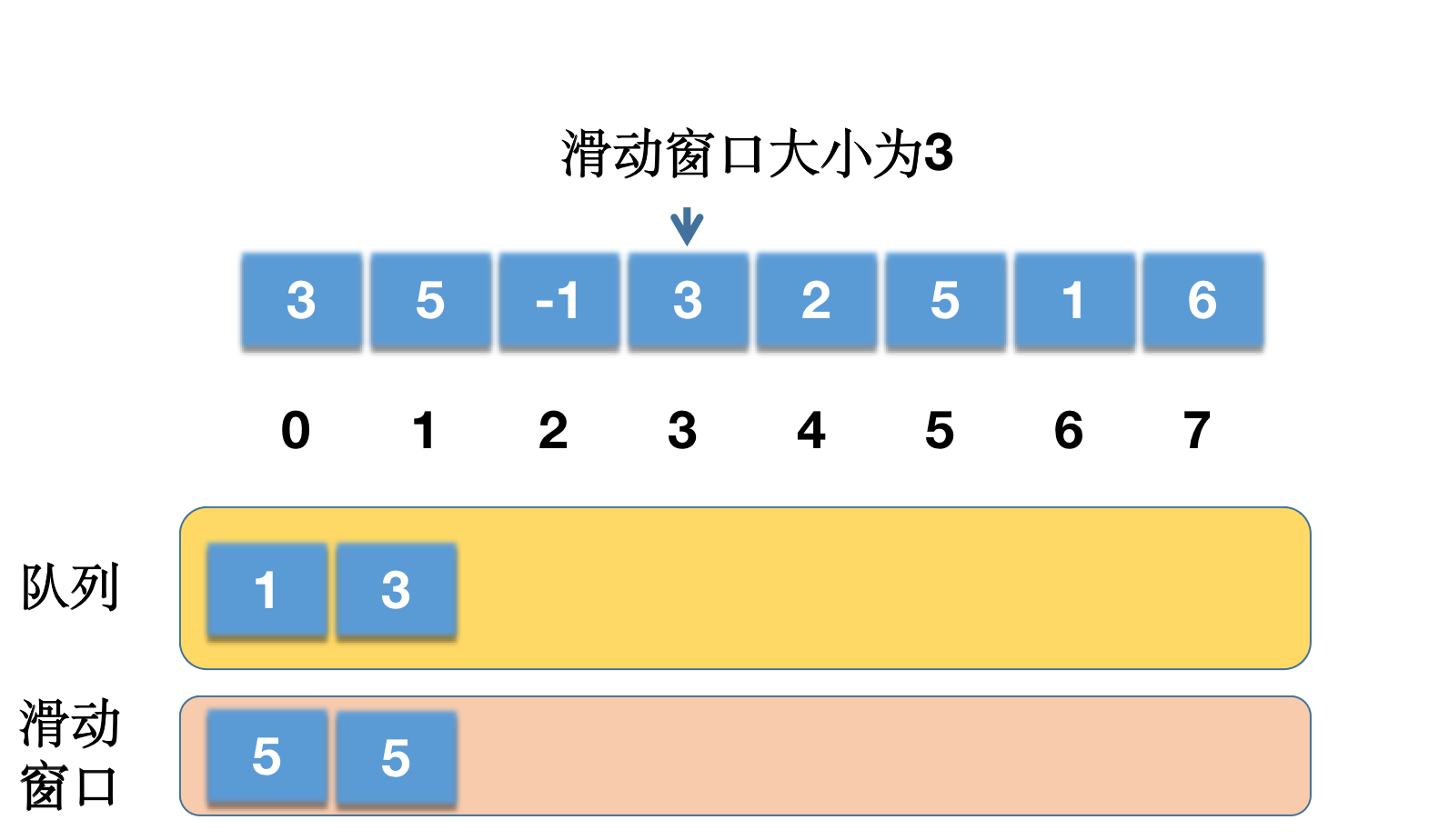
  • i = 4，nums[4] = 2，当前队列为 { 1， 3 }，队尾元素为 3，nums[3] 为 3，nums[4] < nums[3]，因此不需要移除队列尾部的索引元素，直接将当前索引位置 4 加到队列中。队列变成 {1，3，4}，队列的第一个元素（设为 first）为 1，索引为 1 的元素已经不在当前窗口（i-k >= first），需要移除队列头部元素，因此队列变成 { 3，4 }，i >= k-1 满足，因此 results[i-k+1] = results[4-3+1] = results[2] 的值为以队列的第一个元素 3 （当前队列第一个元素）为索引的数组元素，即 nums[3] = 3，因此 results[2] = 3。

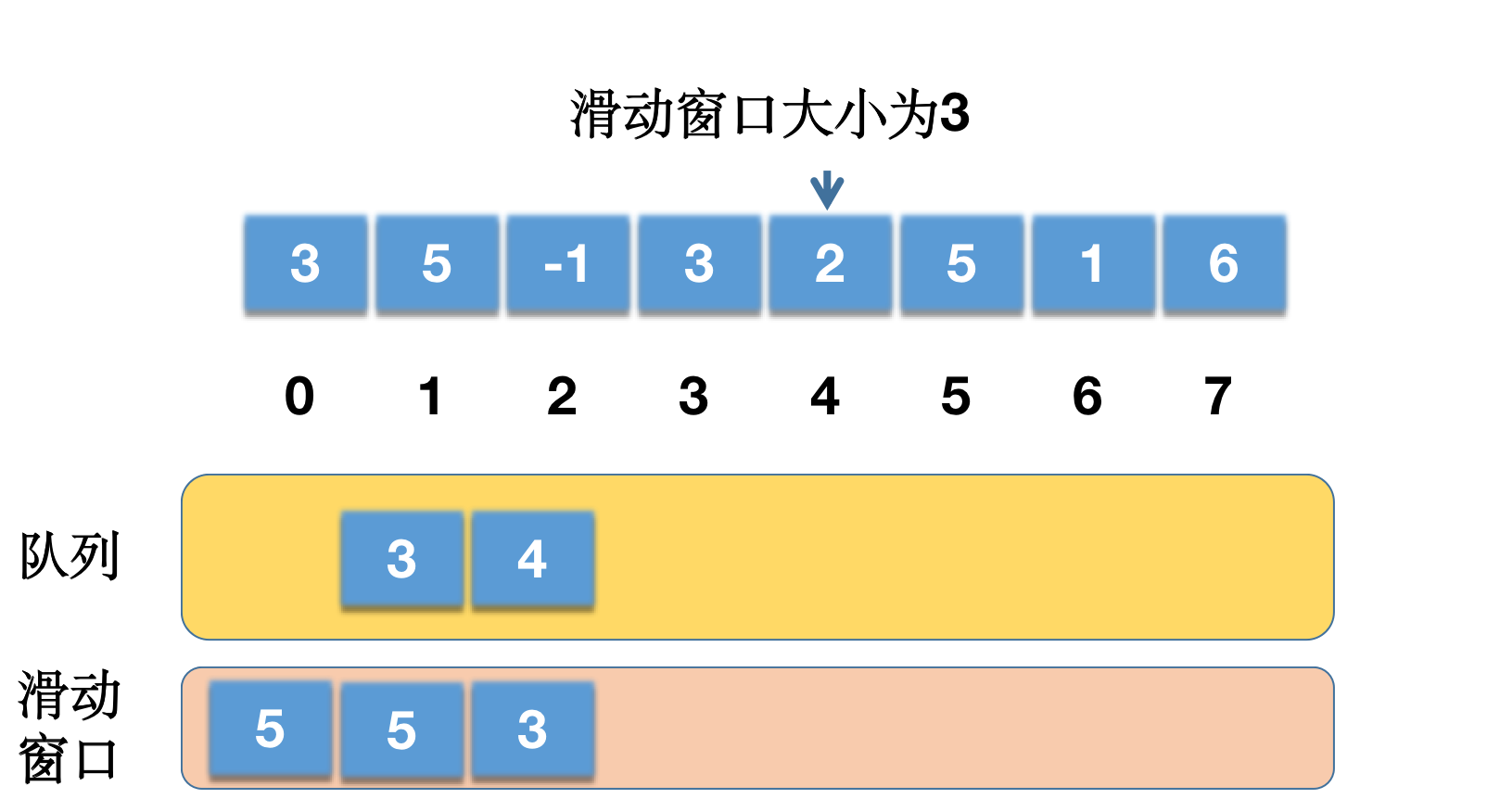
  • i = 5，nums[5] = 5，当前队列为 {3，4}，队列不为空，队尾元素为 4，nums[4] = 2 < nums[5]，因此需要移除队尾元素 4。队列变成 {3}，队尾元素为 3，nums[3] = 3 < nums[5]，因此还需要移除队尾元素 3，队列为空 {}。接着将当前索引 5 添加到当前的队列中，队列为 {5}，队首元素是 5，处在当前有效窗口内，i >= k-1 满足，因此 results[i-k+1] = results[5-3+1] = results[3] 的值为以队列的第一个元素 5（当前队列第一个元素）为索引的数组元素，即 nums[5] = 5，因此 results[3]=5。

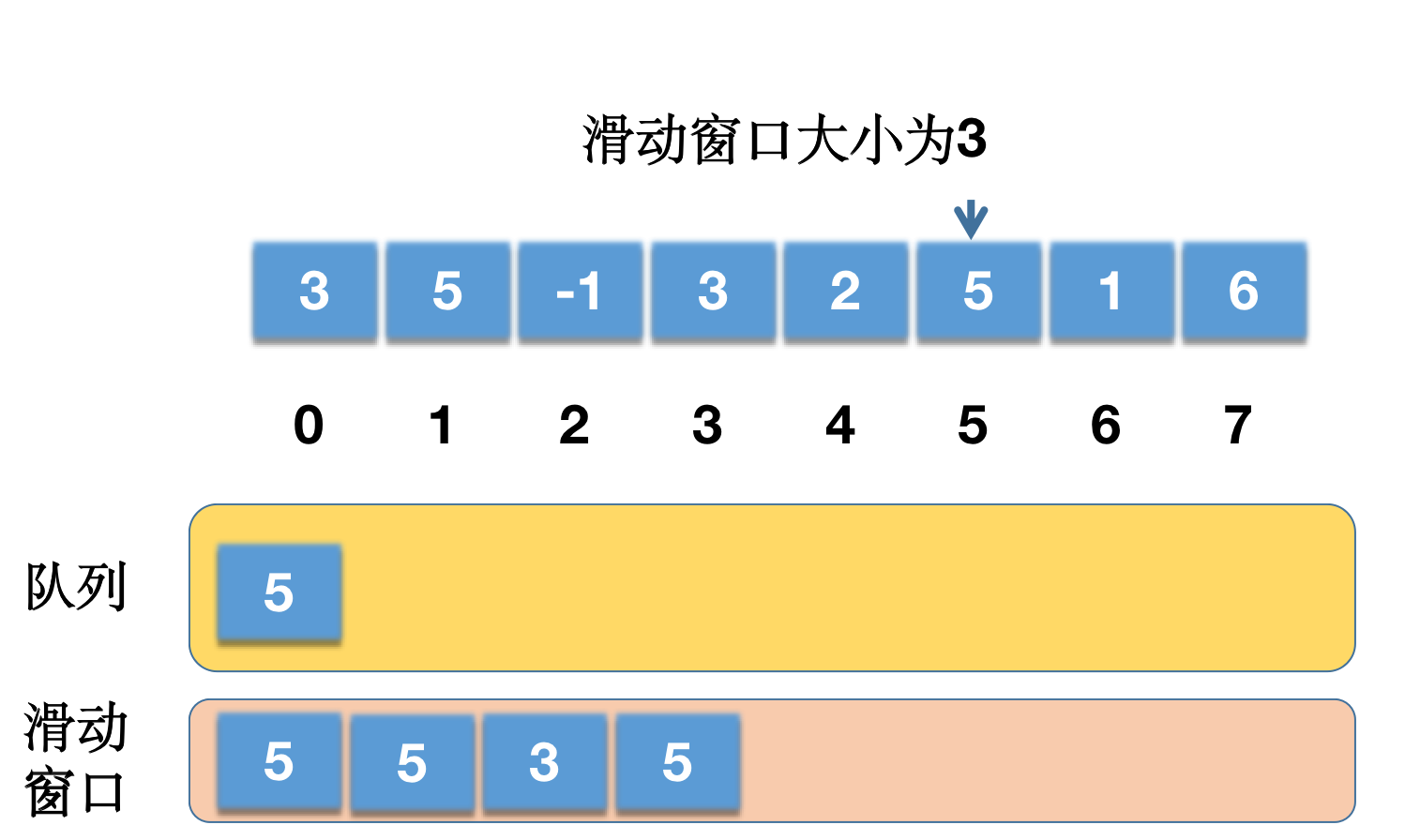
  • i = 6，nums[6] = 1，当前队列为 { 5 }，队列不为空，队尾元素为 5，nums[5] = 5 > nums[6]，因此不需要移除队尾元素。直接将当前索引 6 添加到队列中，队列变成为 { 5，6 }，队首元素为索引 5，当前索引 i = 6，处于有效窗口内，因此不需要移除队首元素。i >= k-1 满足，因此 results[i-k+1] = results[6-3+1] = results[4] 的值为以队列的第一个元素 5 (当前队列第一个元素)为索引的数组元素，即 nums[5] = 5，因此 results[4] = 5。

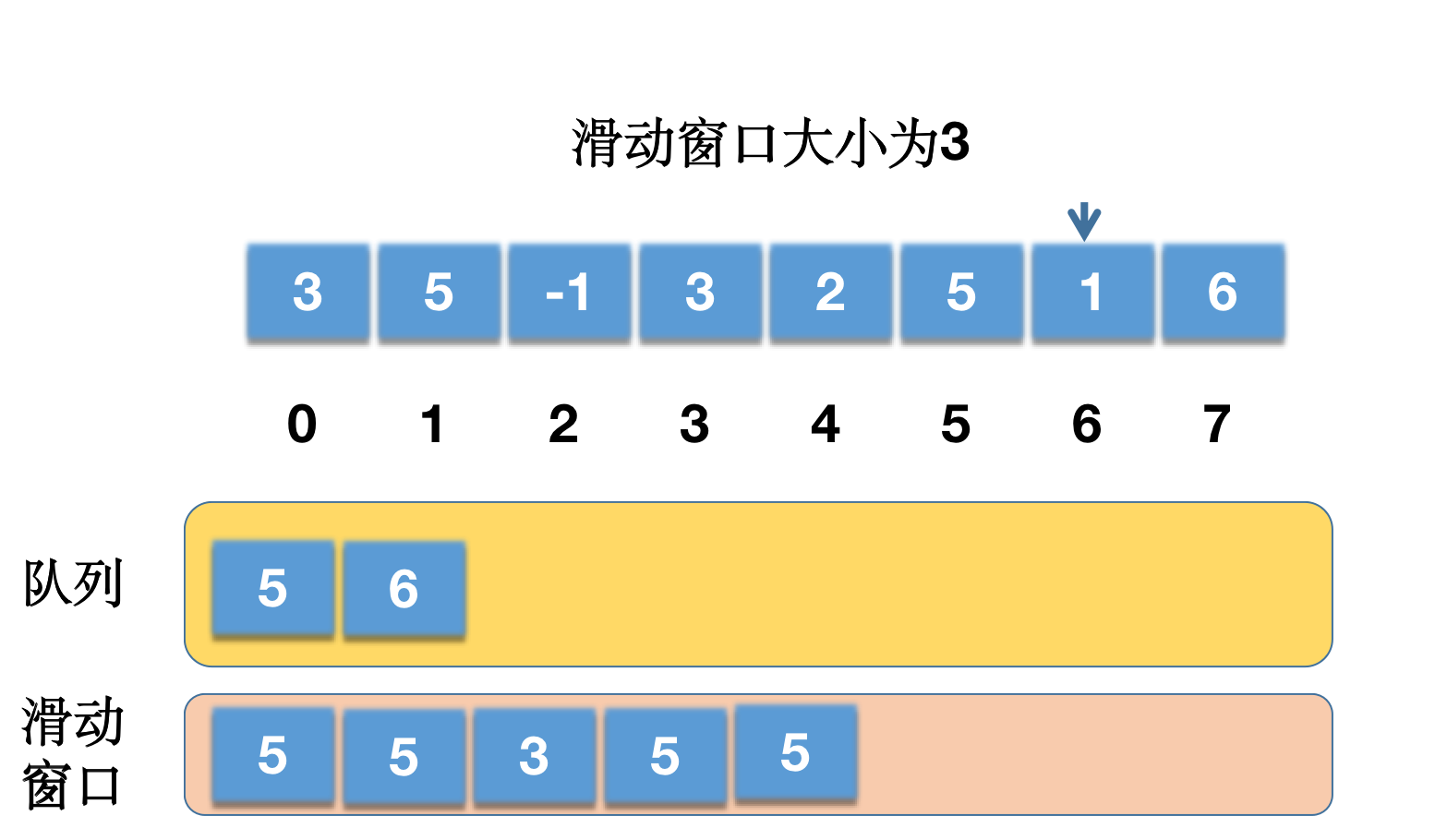
  • i = 7，nums[7] = 6，当前队列为 { 5，6 }，队列不为空，队尾元素为 6，nums[6] = 1 < nums[7]，因此需要将队尾元素移除，队列变成 {5}，当前的队尾元素为 5。nums[5] = 5 < nums[7]，因此还需要将队尾元素移除，此时队列为空 {}，直接将当前的索引 7 添加到队列尾部，队列变成 {7}，队首元素为 7，索引为 i = 7，处于有效的滑动窗口内，因此不需要移除队首元素。i >= k-1 满足，因此results[i-k+1] = results[7-3+1] = results[5] 的值为以队列的第一个元素 7 (当前队列第一个元素)为索引的数组元素，即 nums[7] = 6，因此 results[4] = 6。

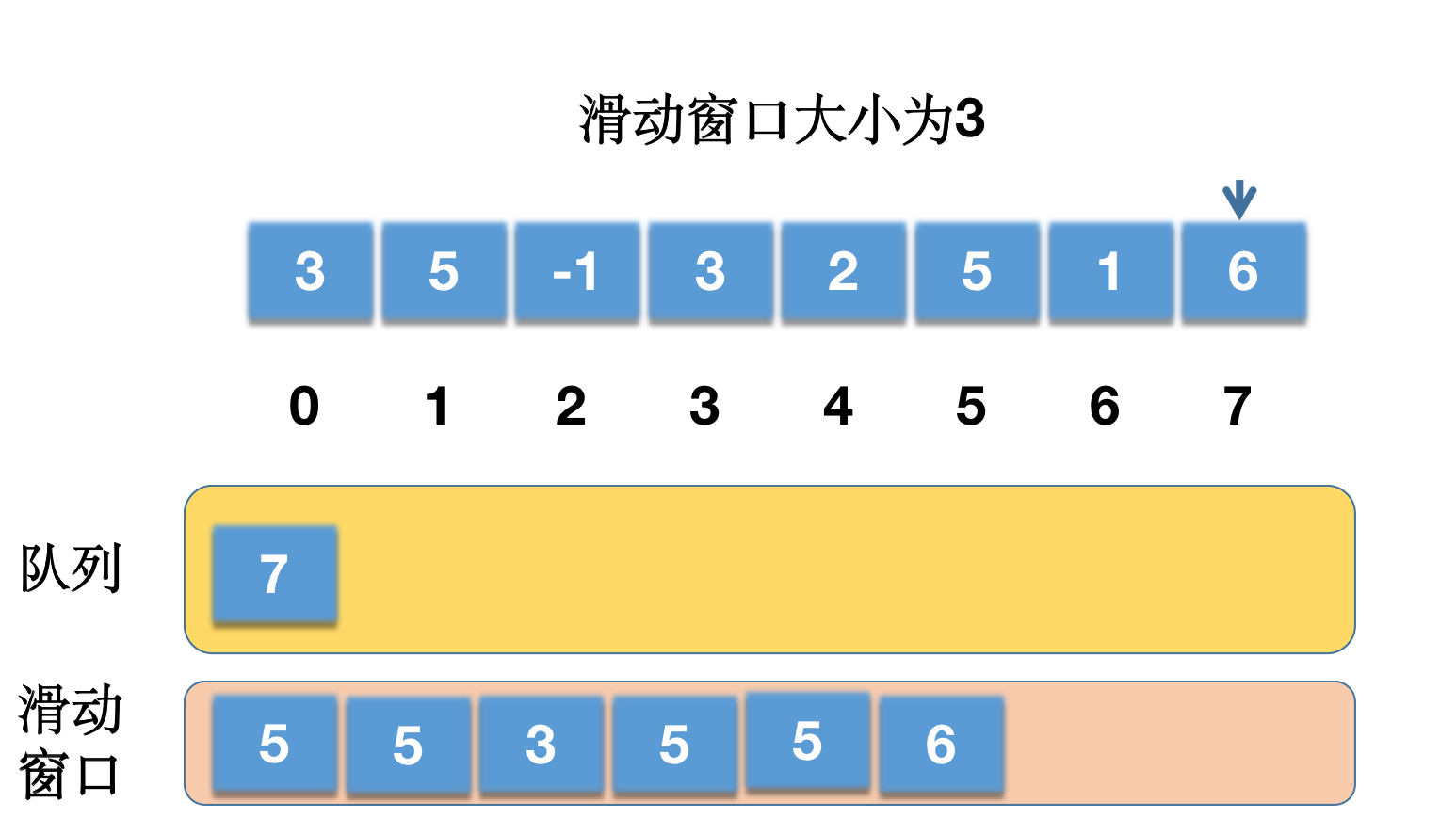
  • i = 8，超出数组范围，结束。

代码实现

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function (nums, k) {
    // 单调下降的队列，最大值就是对头元素
    let res = [];//保存答案
    let queue = [];//要维护的队列,队列中存的数组下表，不是数组元素
    let len = nums.length;
    for (let i = 0; i < len; i++) {
        while (queue.length && queue[0] <= i - k) queue.shift();//超出了k的窗口长度，弹出对头元素
        //进来的元素>=队尾元素，就将从队中元素弹出，他因为他永远不可能是答案
        while (queue.length && nums[queue[queue.length - 1]] <= nums[i]) queue.pop();

        queue.push(i);
        // 从下标是k-1的时候就开始插入
        if (i >= k - 1) res.push(nums[queue[0]]);
    }
    return res;
};

找链表的倒数第k个元素

问题描述

输入一个链表，输出该链表中倒数第k个节点。

求解思路

首先想到的方法，先用一个指针，从头到尾走完，并且边走边计数，可以获得链表的长度 n。然后再使用一个指针又从头开始，走到 n-k+1 的位置，就是倒数第 k 个元素。但是这样就需要遍历两次，并不优雅。

因此我们可以让两次遍历一起进行，也就是两个指针，一前一后，前后指针，先让第 1 个指针先走 k 步，然后第 2 个指针开始与第 1 个指针一起走，直到第 1 个指针走到最后的位置，此时第 2 个指针停留的位置就是倒数第 k 个元素。

代码实现

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
 var getKthFromEnd = function(head, k) {
    let fast=head
    let slow=head
    
    while(fast && k>0){
        fast=fast.next
        k--
    }
    if(!fast) return head.next
    while(fast){
        fast=fast.next
        slow=slow.next
    }
    return slow
};

判断一个链表是否有环

问题描述

给一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

求解思路

如果我们让一个快指针每次走两步，慢指针每次走一步，如果快慢两个指针能够相遇的话，说明快指针走过环并且已经从后面追上了慢指针，那就可以证明环的存在了。如果没有环，那么快指针会直接走到链表的尾部，到达 null 节点，此时链表肯定不存在环的。

代码实现

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
  // 快慢指针初始化指向 head
  let slow = head;
  let fast = head;
  // 快指针走到末尾时停止
  while (fast && fast.next) {
    // 慢指针走一步，快指针走两步
    slow = slow.next;
    fast = fast.next.next;
    // 快慢指针相遇，说明含有环
    if (slow == fast) {
      return true;
    }
  }
  // 不包含环
  return false;
};

两个链表的第一个公共节点

问题描述

现在有两个链表（没有环），但是存在着共同的部分，找出它们的第一个公共结点，例如，下面的两条链表

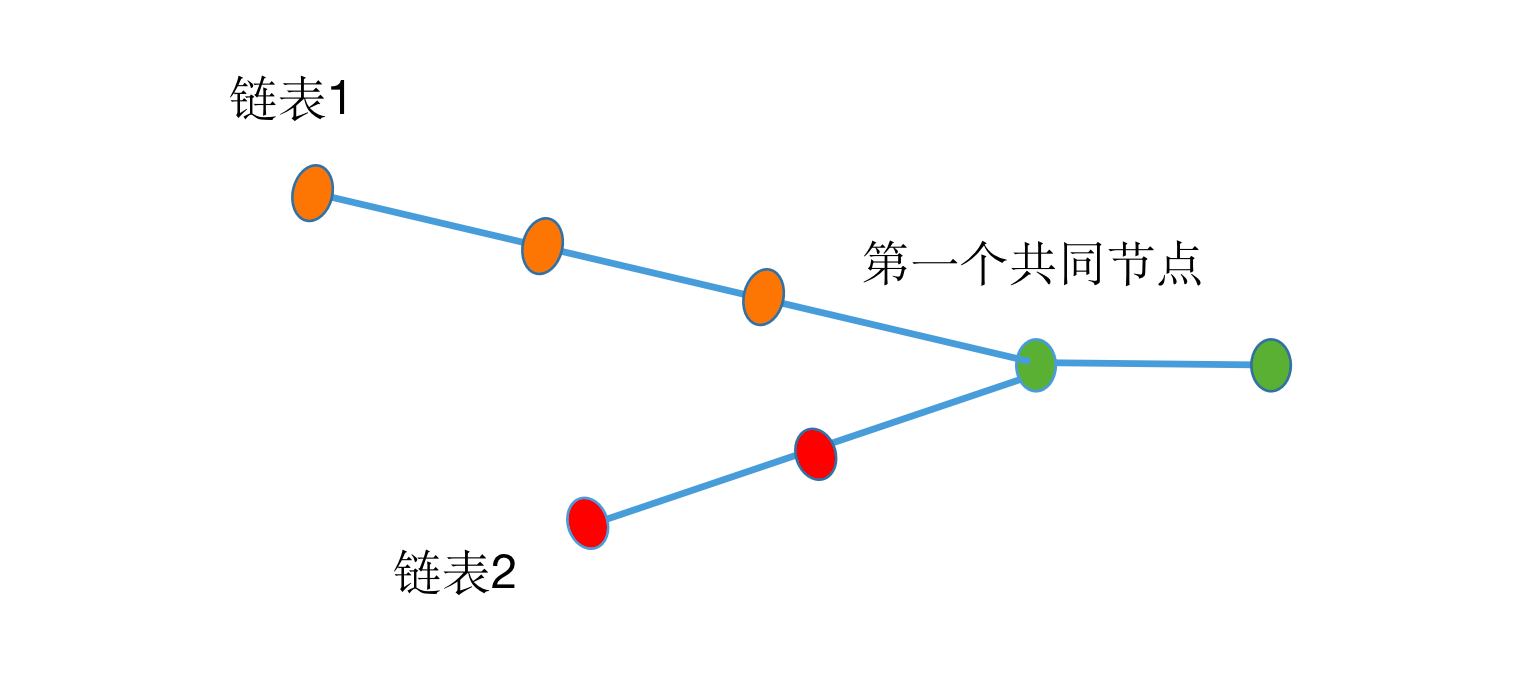
求解思路

从图中我们可以得知，其实从相同节点开始，后面那部分链表都是相同的，也就是如果链表可以从后面开始遍历的话，同时移动，就可以获取到相同的节点。但是明显不能从后面开始遍历，那总得想办法从前面开始遍历时，能同时到达共同节点。

于是，第一个链表后面拼接上第二个链表，第二个链表后面拼接上第一个链表，链表等长了，而且相同的那个元素的位置一样，都在倒数第 2 个

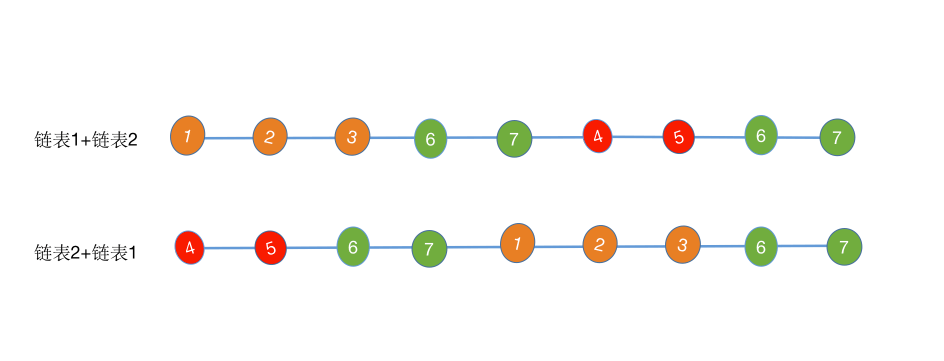
第一个和第二个链表都从第一个节点开始比较，只要相等，就说明是第一个公共节点（即是节点 6）

代码实现

const getIntersectionNode = (A, B) => {
    let pA = A,
        pB = B;
    while (pA !== pB) {
        // 如果下一个节点为空，则切换到另一个链表的头节点，否则下一个节点
        pA = pA === null ? B : pA.next;
        pB = pB === null ? A : pB.next;
    }
    return pA;
};

反转链表

问题描述

给一个链表，要求反转链表后，输出新链表的表头节点。

求解思路

只需要使用循环，不断把指向下一个的指针，指向前面的节点。

假设链表是 1 -> 2 -> 3 -> 4，那么我们需要在开始的时候借助一个 null 节点，当 head 节点不为空的时候，先保存 head 的下一个节点，然后将 head 的 next 指向修改为指向反向，然后移动 head 指针

代码实现

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */

var reverseList = function(head) {
    let last=null
    while(head!=null){
        let nexthead=head.next
        head.next=last 
        last=head
        head=nexthead;
    }
    return last
};

合并有序链表

问题描述

假设两个单调递增的链表，我们要把它们合成一个链表，合并之后的链表需要保持递增的性质，返回头节点，这该怎么做呢？

求解思路

创建一个 -1 节点的新链表，然后两个链表都从头开始遍历，循环直到一个链表遍历到最后，在这个过程中，哪一个链表的节点小，就加入新的链表后面，移动到后面一个节点，接着比较。

之后遍历两个链表剩下的元素，这些元素肯定比另一个链表的所有元素都大或者相等，直接加入新的链表后面即可。

代码实现

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
 var mergeTwoLists = function(l1, l2) {
    // 创建-1头节点
    const prehead=new ListNode(-1)
    let prev=prehead
    // 只要不为空，则比较
    while(l1!=null && l2!=null){
        // l1的节点更小
        if(l1.val<=l2.val){
            prev.next=l1
            l1=l1.next
        }else{
            prev.next=l2
            l2=l2.next
        }
        // 新链表指针后移
        prev=prev.next
    }
    //l1和l2有剩余元素全部加入
    prev.next= l1 === null? l2 :l1
    return prehead.next
};